多変量統計的プロセス管理とは？

統計的プロセス管理 (SPC)

生産プロセスは，指定された仕様を満たす製品を安定して生産できるように維持管理されなければならない．仕様は製品品質に対して定められるため，品質が仕様を満たしているかどうかは，品質測定値を監視することによって確認できる．ところが，品質監視によって，仕様を満たさない製品を見付けることはできても，仕様を満たさない製品が生産されるのを防ぐことはできない．製品品質は生産プロセスの運転の結果であるから，プロセスの運転状態が品質を決める要因となっているはずである．したがって，仕様を満たさない製品が生産されてしまうことを未然に防ぎ，生産性を向上させるためには，品質のみならず，運転状態を監視する必要がある．統計的手法を利用して運転状態の監視を効率的に実施するための方法が，統計的工程管理あるいは統計的プロセス管理（Statistical Process Control; SPC）である．

運転状態は温度や圧力などのプロセス変数によって特徴づけられるため，各測定変数に管理限界を設定し，その管理限界内に測定値があるかどうかで，プロセスが正常に運転されているかどうかを判断すれば良い．この目的で利用されるのが，W.A. Schewhartによって考案された管理図である．品質や運転状態のバラツキには，偶然原因によるものと見逃してはならない異常原因によるものがある．管理図は，統計的な検定を利用して，バラツキが偶然原因と異常原因のどちらによるものかを判断する．例えば，広く利用されている３σ法は，管理したい変数または統計量の平均をμ，標準偏差をσとするとき，管理限界をμ±３σと設定する方法である．もし変数が正規分布に従うのであれば，正常時に測定値がこの管理限界を超える確率は0.27%程度であり，正常時にはあまり起こらない状況と言えよう．したがって，測定値が管理限界を超えれば，それは異常原因によるものだと判断し，原因の特定と対策を実施することになる．

一変量統計的プロセス管理の問題点

管理効果の高い変数は，品質に大きな影響を与え，かつ測定が容易な変数であるが，できるだけ早い段階で異常を検出し，その原因を特定するためには，多くの変数を同時に管理するのが有効である．このため，統計的プロセス管理として，すべての測定変数に対して管理限界を設定することが多い．

このように多くの変数を同時に管理する場合，一変数を管理するための方法である一変量統計的プロセス管理（Univariate Statistical Process Control; USPC）を，そのまま利用して良いのだろうか．ある変数の測定値が正常時に管理限界を超える確率は0.27%程度だとしても，管理する変数が100個もあれば，運転員はアラームの洪水に溺れ，本当に異常が発生したときに適切に対応できないのではないだろうか．さらに，変数を個別に管理する場合，変数間の相関関係は無視されてしまう．例えば，図(a)のように2変数が正の相関を持つとき，USPCの管理限界は相関関係に関係なく矩形となるため，☆印の異常値を検出することができない．

多変量統計的プロセス管理 (MSPC)

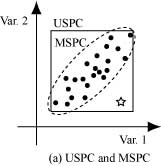
ところが，図中に破線で示した楕円のような管理限界を設定することができれば，変数間の相関関係を捉えたプロセス管理を実現でき，☆印の異常値も検出できる．このように変数間の相関関係を考慮して高度な管理を実現するための方法が，多変量統計的プロセス管理（Multivariate Statistical Process Control; MSPC）であり，主成分分析（Principal Component Analysis; PCA）などの多変量解析が利用される．

MSPCで利用される多変量解析の多くは，ケモメトリクスと呼ばれる分野で利用されている手法である．ケモメトリクス（Chemometrics）とは，化学（Chemistry）と計量学（Metrics）を組み合わせた造語で，統計的手法を利用して化学システム・プロセスの測定データと状態を結び付ける科学である．元々，ケモメトリクスは分析化学の一分野であり，分光分析におけるスペクトルデータ解析などに適した統計的手法が開発された．その後，統計的手法の適用範囲が拡大し，特に化学プロセスデータを対象とする場合にプロセスケモメトリクス（Process Chemometrics）と呼ばれるようになった．

主成分分析に基づく多変量統計的プロセス管理 (PCA-MSPC)

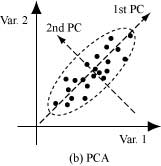
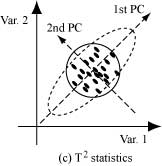
PCAを利用することによって，図(b)のような管理限界を設定できる．しかし，このままでは管理限界を超えたかどうかの判断を簡単に行うことができない．そこで，Hotelling's T2統計量を用いる．T2統計量は，規格化された空間での原点からの距離に対応している．この統計量を利用することによって，図(c)のように，管理限界を楕円から真円に変形することができるため，正常と異常を区別するのに適した上限値をT2統計量に対して設定すれば良い．

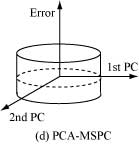
PCAとHotelling's T2統計量を利用するSPCは，Jacksonによって最初に提案された．ただし，提案法ではPCAによる次元圧縮は行われておらず，T2統計量の利用が主要なテーマであった．その後20年を経て，PCAによる次元圧縮を実施した上で，主成分で張られる部分空間とその直交補空間を独立に管理する方法が登場した．この新しい管理方法の概念を図(d)に示す．主成分で張られる部分空間については，T2統計量による管理が有効である．一方，その直交補空間については，残差から計算されるQ統計量を用いて管理する．Q統計量は二乗予測誤差（Squared Prediction Error; SPE）とも呼ばれ，データのうち，PCAモデルによっては表現できない部分を表す．T2統計量とQ統計量を同時に監視し，いずれか一方でも管理限界を超えた場合に異常と判定するのが，主成分分析に基づく多変量統計的プロセス管理（PCA-MSPC）である．